El avistamiento de un OTNI (Objeto Taurino no Identificado) provoca una investigación de la ARMY y la Nasa que concluye con la solución del misterio
Fue hace un año, 22 de Junio d 2014, en Sevilla, En el quite con el capote a la espalda el del Conde de la Maza no obedeció al capote. El utrero se vino de largo, galopando con son. Al llegar a la jurisdicción del torero el toro hizo por él. El encuentro fue violento, el susto tremendo. El torero se levantó sin mirarse y a seguir, que siguió, como si nada...repitiendo el quite, (ver vídeo completo pulsando aquí)
A la misma hora...., el pentágono recibe un aviso.Justo a ese hora, 20.17 desde el observatorio de la base conjunta de Morón alguien observó un Objeto Volante No Identificado. La preocupación fue máxima ¿De que se trataba? Todas las alarmas y tratamiento de secreto de estado.
Tras un año de arduas investigaciones, donde nuestro vídeo ha estado secuestrado, el alto comisionado, con ayuda de la NASA encuentra explicación, a través de un expediente TOP SECRET,. Se trata de la zapatilla de David de Miranda.
¿Pero, a que altura llegó la zapatilla?
Si suponemos, calculo realizado tras medir el desplazamiento del toro desde las rayas de picar hasta los medios, que en el momento del impacto del toro contra el torero la velocidad era de 25 Kms/hora y que el impacto trasladó esa velocidad, multiplicada por un factor de correccional de 1.5, al pié del torero. Habida cuenta que sabemos el tiempo transcurrido desde que la zapatilla sale volando, 2.6 s, el espacio recorrido, y la aceleración provocada por la fuerza de la gravedad. La zapatilla de Miranda alcanzó los 7 metros y medio (7.5mts) de altura (error de +/- 5%) en el cielo sevillano de aquella tarde y pudo ser divisada por los sofisticados sistemas de detección de la base aerea de Morón, por cierto justo al lado de donde se había criado y había vivido el toro del Excmo.Señor Conde de la Maza que provocó el fenómeno.
Justificación matemática facilitada por la NASA
Suponiendo que se tratará de un movimiento rectilíneo uniformemente acelerado
Dado que la velocidad no permanece constante pero sí sus variaciones podremos escribir:
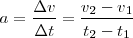
Si consideramos que en un instante cualquiera 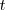 el móvil lleva una velocidad
el móvil lleva una velocidad  , y fue
, y fue 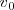 la velocidad con la que inició el movimiento, es decir la que tuvo en el instante
la velocidad con la que inició el movimiento, es decir la que tuvo en el instante 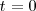 , tendremos:
, tendremos:
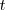 el móvil lleva una velocidad
el móvil lleva una velocidad  , y fue
, y fue 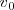 la velocidad con la que inició el movimiento, es decir la que tuvo en el instante
la velocidad con la que inició el movimiento, es decir la que tuvo en el instante 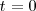 , tendremos:
, tendremos: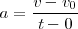
o lo que es igual
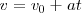
obteniendo para la velocidad una función lineal de 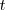 en la cual es la aceleración
en la cual es la aceleración  el coeficiente de la variable. Al representar la recta obtenida tendremos en cuenta que su pendiente igual a
el coeficiente de la variable. Al representar la recta obtenida tendremos en cuenta que su pendiente igual a 
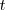 en la cual es la aceleración
en la cual es la aceleración  el coeficiente de la variable. Al representar la recta obtenida tendremos en cuenta que su pendiente igual a
el coeficiente de la variable. Al representar la recta obtenida tendremos en cuenta que su pendiente igual a 
Por otra parte, podremos calcular la velocidad media 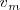 de la partícula dividiendo el espacio total recorrido por el tiempo empleado en recorrerlo, es decir:
de la partícula dividiendo el espacio total recorrido por el tiempo empleado en recorrerlo, es decir:
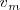 de la partícula dividiendo el espacio total recorrido por el tiempo empleado en recorrerlo, es decir:
de la partícula dividiendo el espacio total recorrido por el tiempo empleado en recorrerlo, es decir: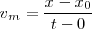
y por lo tanto
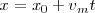
Por otra parte, dado que las variaciones de la velocidad son directamente proporcionales al tiempo, podremos escribir para la velocidad media:
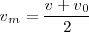
y sustituyendo en la ecuación precedente:
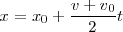
Sustituyendo  por su valor en función de la aceleración y del tiempo:
por su valor en función de la aceleración y del tiempo:
 por su valor en función de la aceleración y del tiempo:
por su valor en función de la aceleración y del tiempo: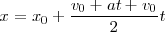
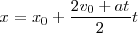
con lo cual
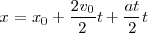
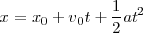
Como vemos, la ecuación obtenida para el espacio recorrido en un instante 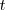 es una función del cuadrado del tiempo, y su representación gráfica en función del tiempo será una parábola, cuya tangente en cada punto tendrá por pendiente el valor de la velocidad.
es una función del cuadrado del tiempo, y su representación gráfica en función del tiempo será una parábola, cuya tangente en cada punto tendrá por pendiente el valor de la velocidad.
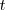 es una función del cuadrado del tiempo, y su representación gráfica en función del tiempo será una parábola, cuya tangente en cada punto tendrá por pendiente el valor de la velocidad.
es una función del cuadrado del tiempo, y su representación gráfica en función del tiempo será una parábola, cuya tangente en cada punto tendrá por pendiente el valor de la velocidad.
Si eliminamos el tiempo entre las ecuaciones de la velocidad y del espacio:
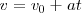
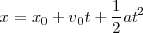
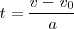
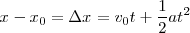
sustituyendo 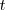 por el valor obtenido en la ecuación de la velocidad
por el valor obtenido en la ecuación de la velocidad
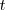 por el valor obtenido en la ecuación de la velocidad
por el valor obtenido en la ecuación de la velocidad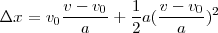
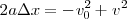
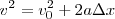

No hay comentarios:
Publicar un comentario